Suppose you want to create a generation machine to determine what a hex contains: people, monsters, topography, vegetation, defenses, dungeons, what have you. You could put together a simple linear table that would have a list of results: on a d100, a 01-03 indicates a single dwelling, a 04-06 indicates a thorp, a 07-09 indicates a hamlet, and so on - the DMG proposed just such a table. The number of results could be increased well past 100 possibilities, by having the list on a d1000 or even a d10000. Just creating 10,000 possible results could take some time.
But suppose you would rather have the results appear more towards a bell curve: upon 3d6, some kind of settlement could occur upon a 10 or an 11, while pure wilderness would occur upon a 3 or an 18 ... with varied gradients appearing with other numbers. The avid creator could try 3d100 or 3d1000, assigning results according to the bell curve as desired.
It would be nice, however, if the bell curve could depend upon some central theme, and that the theme would give us a sense of the hex contents, as well as the purpose the hex serves in the greater picture of the generated wilderness ... after all, we are not merely generating one hex, but potentially hundreds, and it would be nice if somehow the generation thereof produced a cohesive result.
Very well, let's try something simple.
Suppose we take a hex, and we carve it up into seven smaller hexes, like so:
There's nothing at all unusual about this picture. For game purposes, its usually assumed that the blank areas between the hexes are 'covered,' and that the hex pattern is an identifying convenience. We can see that seven hexes fit inside the first hex, and that these seven hexes could be considered zones A to G or 1 to 7 ... or Alpha-Bravo-Charlie-Delta-Echo-Foxtrot-Golf if you like. For the moment it doesn't matter. For the purpose of this document, I'm more concerned with the designation between the large, greater hex and the seven lesser hexes within. I could go with greater and lesser, but for greater clarity I'm going to go with Senior and Junior. Thus, there is one Senior hex and seven Junior hexes.
Suppose we then define each junior hex as one of two things: habitable or non-habitable. For our purposes, we can say habitable is arable and easily accessible - so fields, meadows, well-watered flats, glades, what have you. We can then consider non-habitable as rocky, dangerous, overgrown, flooded or filled with sand dunes.
We can then postulate that any of the seven junior hexes is either 'H' or 'non-H' ... and this gives us a number of base possibilities equalling 2 to the 7th power, or 128.
Not a huge number. Moreover, I must argue that the actual number of possibilities is much smaller ... but let's leave that go for the moment.
Immediately and right off, we can consider the best possible arrangement to be where every junior hex is H. That provides the most arable land and the greatest food production ... and the greatest ease of travel. Roads are cheap to build and cart-tracks are everywhere. We can assume that such an area is well-watered, and probably that there is some kind of significant conglomeration of people. How significant would probably be determined by the amount of arability in adjacent hexes - for now, let's just say that any hex that is all arable contains a Town ... which would be 1 in 128 hexes.
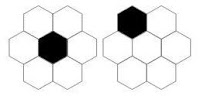
Now suppose we look at groups (or 'groupings,' as opposed to 'patterns') where just one junior hex is non-H:
Odds are 7:128 of getting just one non-H hex, but there are only two possible groups... and the group on the left (A) is six times less likely to occur than the group on the right (B). Consider what either might mean.
For that, I propose that any 'habitable' might be a designation used properly just with humans; if there's going to be a dungeon, or some dangerous lair, or some evil element in the senior hex, its going to be in the black patch above.
Consider that for Group B three of the junior hexes are removed from the non-H hex, so that they can be protected by those three hexes that are adjacent. Of course, the next senior hex over might be filled with non-H hexes, but let's disregard that. Group B is at least somewhat 'gathered' together, in that there is a central region that can be protected and even be considered almost as good as lacking non-H hexes altogether. A good sized village or small town can easily be imagined to fit here.
But Group A is a mess. The central non-H hex dominates the senior grouping, disrupting communication between H hexes across from one another. Surely this must indicate some unique situation: perhaps a holy religious centre, or a reclusive fortification, surrounded by cliffs or swamps. It's hard to imagine anything but rough hamlets surrounding the central hex.
Let's move onto hexes where two junior hexes are non-H:
Odds here are 21:128, but in fact there are four possible patterns. Turn them around however you wish, the groups only occur as above. From left to right, call them A, B, C and D.
A & D are notable in that the non-H hexes are adjacent, creating larger dangerous regions. Group D especially reduces communication between two of the H hexes, suggesting those hexes might be arable, but backward and probably poorer. Group A allows for the greatest conglomeration of good transport and land ... in that way, it offers the best opportunities for a good habitation.
Group B has four hexes gathered together, so that might be a village, but at least part of the senior group would be represented by some sort of backward sort, cotters and rustics reached by a somewhat dangerous road, beset by two areas from which bandits or who knows what else might emerge. Group C could be some sort of pass, or perhaps a ford along a dangerous river (the black areas could be swamps along a river coarse), making it an important military post, or transshipment point.
After all, the black areas may not be woods, swamps or mountains at all: they could represent an ocean or a lake. There are many possibilities. Thus Group C could be Corinth, an isthmus between two seas.
Let's continue; you'll certainly be getting the idea now.
Both Groups E and F feature hexes that are completely removed; any such arrangement would probably indicate some kind of border or boundary, potentially one for language and culture as well as for political authority. A road through such a group would be rare.
At any rate, you can see how the conglomeration of good hexes affects the overall picture to the positive or the negative. Once the arrangement is identified as being a mass of wilderness, or civilization, the logic of what should occupy the hex - and even the adventuring within - becomes evident. And this is with just two options. Suppose you were to designate the junior hexes with three possible results for each, rather than two - well, the possible arrangements would soar to 2,187. There wouldn't be any point in that, however, unless you could define what all those permeatations meant ... and once again, that could take some time.
But you could establish the meaning of any combination - so that even if you designated a junior hex could be either friendly humanoid, enemy humanoid, deserted or with a big bad (4 to the 7th power, 16,384 possible combinations), then even if you couldn't predict every possibility, you could look at two adjacent hexes and know what was there. And where to take it with a session should the party enter the senior hex.
Oh, I should post the remaining possible groups. Those that remain are just negatives of those above:
Incidentally, I stumbled across this idea tonight, as I was conjecturing how to design a hex-filling generator, and I thought I'd go ahead and write a post about this in the hopes of inspiring some further advice. To me, it seems a good way to build a strong bell-curve to construct a randomized world. Yes, I have presented the above discussion as though the groups might be isolated. I recognize that an expanse of differently generated hexes should create patterns that would go beyond just the junior hexes. Moreover, you could easily tweak the pattern by having H hexes turn up slightly more commonly than non-H hexes (or the reverse), changing the amount of tweak for one continental area vs. another (Europe vs. Africa).
It is just the kernal of an idea, I think. It needs a grander, unifying approach.



>>It is just the kernal of an idea, I think. It needs a grander, unifying approach.
ReplyDeleteIt is one of the greatest kernels of idea I've seen recently. I'm preparing to my new sandbox campaign right now and you got me seriously thinking of either going with your 1 senior - 7 junior hexes approach or using it in my 1 senior - 19 junior (like traditional 25 mile hex).
Great idea!
I'm thinking about printing the combinations on 3x5 cards to create a deck than could be shuffled and dealt out for a quick area map. You could tweak the layout or pick them up and re-deal until you get something you like.
ReplyDelete(Clearly a piece of software would be faster, but my programming skills are not up to that at the moment.)