Better

 My partner and I don't celebrate Valentine's Day, so ...

Going to get fairly self-indulgent here, as I explain what's going on with the above.  This is still in the draft stage; but I'm far enough that I feel I want to keep going.  But as others are interested, I'll take some time to explain what's going on.

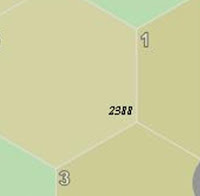
But first, I've gone back to the old colour scheme.  The above is a "2-mile" map; each hex is 2.22 mi. in diameter.  The above shows the expansion of six mile hexes surrounding Garalzapan's land. 

Here's an image of the 6-mile map covering the same area:

Sf

And to the right is the same area, as it appears on the 20-mile map.  Isn't it nice that a section of blank map can be transformed into something tactile and interesting?  Sorry, that's self-aggrandising.  I'll resist.

The hex marked "2388" has an infrastructure of 46.  This can be distributed in a number of ways, but in the case of Garalzapan's land, it produced one "type-3" hex, three "type-4" hexes and three "type-6" hexes.  How is this distribution calculated?  Well, a type-3 hex costs 16 infrastructure; each type 4 hex costs 8 infrastructure; and each type-6 hex costs 2 infrastructure.  16+8+8+8+2+2+2 = 46.

Potentially, this could have been two type-3 hexes (32), three type-5 hexes (4 each) and a type-6 (2), which also equals 46.  The seventh hex is a type-8, wilderness, no infrastructure.

So, when infrastructure is very high, we get a bunch of type-1, type-2 and type-3 hexes, which appear brown; middling infrastructure hexes get multiple type-4 hexes.  And low infrastructure gets 6s, 7s and 8s.  No infrastructure is all 8s.  Follow?

Okay, showing that Garalzapan type-3, 6-mile hex up close.  The idea is to translate this into 2-mile hexes according to a process that can be applied to any other hex.  For a long time now, I've operated on the principle that a type-3 hex is made of five civilised hexes and two wilderness.  This is the reason it's called a "type-3" hex.  With a type-8, every inner hex is wilderness; with a type-7, one hex is civilised and six are wilderness; type-6 has two civilised hexes, type-5 has three, type-4 has four, type-3 has five.  Get it?

This has been a central core of my mapbuilding logic for 10 years.  And the map I built Saturday was built according to that principle.  But ...

What's been breaking my balls for two days has been what to do with those coins, hammers and food in the upper corner.  How are those distributed among the five civilised hexes a type-3 has?  Are they distributed?  Well, they have to be.  The food is grown somewhere.  The hammers represent labour and the physical results of that labour; the coin is generated somewhere.  But ... how?  I could make some ad hoc table that gives a weight to each hex according to how far it is from the central authority of that hex, in this case, "Garalzapan."  But what about hexes that don't have a village?  How do I distribute them?  Consistently, in every case, regardless of what hex is being sorted?  Is there a different table for each type of hex?  That really seems inelegant.

When the original distribution of 46 infrastructure was made, it looked like this:

This is elegant.  Type the number, the hexes result, they're distributed in order according to the randomly generated hexes below.  This tells me where each type of hex goes.

I wanted something like this ... and only this morning I realized how that was possible.

Look.  A type-3 hex costs 16 infrastructure.  Why not simply input "16" on the table above, and have it generate a distribution of those 16 infrastructure among 2-mile hexes?  And then, reassign hammers, coins and food according to the new 2-mile distribution?  So that's what I did.  And this is what that looks like:

Sorry it doesn't look better, but alas, it's a tiny part of a big picture.  Anyway, the reader may note this has three type-8, or wilderness hexes.  In other words, throwing a ten-year concept into the trash can here.  And I don't give a damn.  The old plan got me here, but when a plan ceases to get us farther, we drop it and move on.  This is a critically important element of design, one that makes it worth my going through all this process chatter that can't possibly matter to anyone but me.  Half the time, in design, we're crippled by something we think has to be so, but in fact has to be pushed out the car door.

We have to talk about translating production now.  I'll remind the reader briefly that one food symbol = 1 food; that two symbols equal 3 food; that three symbols equal 7 food and so on.  This also applies to hammers and coins.  On a 6-mile map, "1 food" will feed 70 people for a year; "1 coin" represents a production of 70 g.p. wealth, which I go into with this post.

Garalzapan's type-3 hex on the 6-mile map showed 3 bread slices, 3 hammers and 2 coin-symbols ... or, 7 food, 7 hammers and 3 coins.

And the type-4 hex on the 2-mile map seems to show the same; but, of course, we've zoomed in.  We've expanded the size of the map by 300%.  How does this apply to the former numbers for food, hammers and coins?

Yes, well ... not as well as I might have hoped.  Adjusting two bread symbols to three more than doubles the number of "food" indicated.   I'm taking the position that each symbol is reduced from representing 70 to "35."  Garalzapan's two coins on the 2-mile map represent only 105 gold ... but the type-5 hex at the top is also Garalzapan's, so that increases the total to 140.

On the other hand, according to the 6-mile map, Garalzapan's land had 7 food and could feed 490 people.  The 2-mile map shows 44 food ... which at 35 persons per food, is enough for 1,540 persons.

The way I see it, the 6-mile hex is an estimate.  A practical shorthand for large parts of the world I intend never to translate into 2-mile hexes (unless I either get rich enough to own a team of creators or I live to 300).  The 2-mile hex is, on the other hand, more accurate.  And that's what I'm going with.

I have a good idea for what to do with the hammers.  As I said, 1 hammer would indicate something like a well, 2 hammers a mill for grinding grain, 3 hammers a storehouse or a shrine.  Garalzapan's total hammers in the hex are 16; I'm just thinking how to assign specific facilities according to the total hammers within each hex ... or possibly, in a circle of seven hexes.  I'll be "hammering" out a formula for this in good time.  I want to give it a bit more thought.

Okay, that about covers it.  What'll we say we get back to worldbuilding now?